Threader: A Constraint-based Verifier for Multi-Threaded Programs

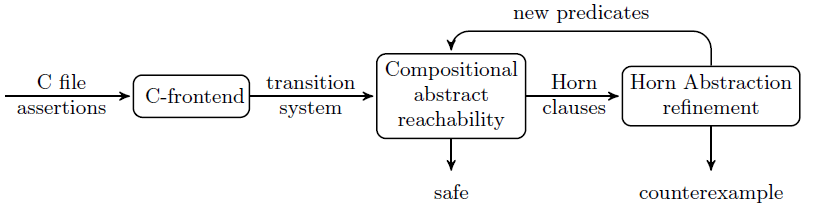
Threader (alias Cream) is a tool that implements Owicki-Gries and Rely-guarantee methods for the compositional verification of multi-threaded programs. Our tool computes the requisite auxiliary assertions automatically using an abstraction and refinement procedure. Our procedure is based on a Horn clause encoding of refinement queries and facilitates the discovery of thread-modular proofs when such proofs exist.[PDF]

Arguments

Input Syntex

• spin2003-tid.c
• spin2003.c
• bakery.simple.c

Example use

int t1=0, t2=0; // N natural-number tickets
int x; // variable to test mutual exclusion

void thr1() {
  while (1) {
    t1 = t2 + 1;
    while( t1 >= t2 && ( t2 > 0 ) ) {}; 
    x=0;
    assert(x <= 0);
    t1 = 0;
  }
}

void thr2() {
  while (1) {
    t2 = t1 + 1;
    while( t2 >= t1 && ( t1 > 0 ) ) {}; 
    x = 1;
    assert(x >= 1);
    t2 = 0;
  }
} 

The two assertions instrument the mutual exclusion property. We first attempt to prove the assertions using monolithic verification:

        ./cream --threads thr1:thr2 --algorithm:monolithic bakery.simple.c

Very likely the monolithic verification will get stuck during abstract reachability. We can then try rely-guarantee reasoning:

        ./cream --threads thr1:thr2 --algorithm:rely-guarantee bakery.simple.c

== Iteration 28 ===================================
Predicates:
P[1]:   #15:    t2-t1=< -1, x=<0, t2>=0, t1>=1, t1-t2=< -1, t2=<0, t1=<1, t1>=0, t1-t2=<0, t1=<0, t2>=1, t1>=2, t1-t2>=2, t1-t2=<1, x>=1
P[2]:   #11:    t1-t2=< -1, x>=1, t1=<0, t1-t2>=1, t1>=2, t2>=0, t1>=1, t1>=0, t2>=1, t1-t2>=0, t1-t2=<1
P[1->2]:        #18:    t1'-t2'>=1, t1'-t2'=< -1, t1-t2+t1'>=1, t2-t1'=< -1, t1=<0, t1-t2>=0, x-x'=<0, t2-t2'=<0, t2=<0,
 t1'-t2'>=0, t1-t2-t1'+t2'=<0, x=<0, t1'>=1, t1>=1, t1'=<0, t1-t2=< -1, t1'-t2'=<1, x'>=1
P[2->1]:        #20:    t1=<0, t1'-t2'=< -1, t1-t2>=1, t1-t2=<0, t1-t2=< -1, t1>=2, t1'=<0, t2-t2'>=0, t1-t2>=0, t1'-t2'
>=1, x-x'>=0, t1-t1'=<0, t1'>=1, t1-t2'=< -1, t2-t2'=<0, t1-t1'+t2'=<0, t1-t2=<1, t1'-t2'=<1, x'>=1, x>=1
Abstract reachability computation...
Abstract reachability computation completed in 266 msec.


==================================================
Program is correct.


==================================================
Verifying fixpoint...done.
Proof wrote in dot format to file: reach.dot.
Time on total                           :               run 2.58,        wall 4.47 s.
Time on result checking                 :               run 0.19,        wall 0.19 s.
Time on total including result checking:                run 2.77,        wall 4.66 s.

An archive file

An archive file that contains:

• Linux x86-32 executables
• collection of multi-threaded test files in the directory ''c_tests''
• regression test suite: ''run_tests.sh''
• collection of sequential test files (obtained from the multi-threaded files by instrumenting thread counter variables ''pc1'', ''pc2'') and scripts to run two state-of-the-art model checkers (Blast and ARMC) on the sequential test files

Feedback is welcome

Please email feedback and comments to Corneliu.